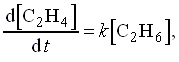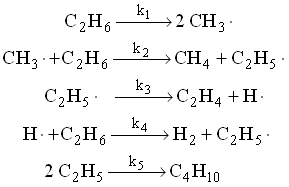Fizikai kémia elõadás
és számolási gyakorlat
.  címoldalhoz
címoldalhoz
Beadandó házi feladatok
1 2 3
4 5 6
7 8 9
10 11 12
13 14

1. feladat: Számítsa
ki, mennyi idõ alatt lehetne meghatározni Avogadro számnyi
darab (6x1023) részecske
energiáját, ha másodpercenként meghatározunk
egy részecskeenergiát. Az eredményt évben adja
be, és hasonlítsa valami nevezetes idõhöz (pl.
emberélet, évszázad, évezred, stb.)
(beadási határidõ:Február 17.)
2.: feladat: Atkins:
Gyakorlatok 19.5
Ismeretes, hogy valamely atom alapállapota
háromszorosan degenerált, a
3500 cm-1-nél lévõ
gerjesztett elektronállapota nemdegenerált, a 4700 cm-1-nél
fekvõ energiaszint viszont ismét háromszorosan degenerált.
Határozza meg ezeknek az elektronállapotoknak az állapotösszegét
1900 K hõmérsékleten.
3. feladat: Atkins:
Gyakorlatok 19.7
Ismeretes, hogy valamely molekulának
a nemdegenerált a alapállapot fölött
540 cm-1-gyel nemdegenerált
gerjesztett állapota van. Milyen hõmérésklet
szükséges ahhoz, hogy az összes molekula 10%-a a nagyobb
energiájú szinten tartózkodjék? (Csupán
e két állapotot kell figyelembe venni.)
5.: feladat: Atkins:
Gyakorlatok 19.2
Határozza meg (a) 300 K; (b) 400 K hõmérsékleten
a 2,00 cm3 térfogatú tartályba zárt,
120 g mol-1 moláris tömegû molekula haladó
mozgásához rendelt állapotösszeget.
(beadási határidõ:
Március 4.)
6.: feladat: Atkins:
Gyakorlatok 19.3
Határozza meg az 1,00 cm élhosszú
kockába zárt argonatom (a) termikus hullámhosszát;
(b) transzlációs állapotösszegét (i) 300
K; (ii) 3000 K hõmérsékleteken.
(beadási határidõ:Március 4.)
7.: feladat: Atkins:
Gyakorlatok 20.11
A Cl atom alapállapota 4x degenerált,
és a 2x degenerált nívó 881 cm-1-gyel
fölötte helyezkedik el. Határozza meg, hogy mennyivel
járulnak hozzá az elektronok a Cl-atomok hõkapacitásához
(a) 500 K; (b) 900 K hõmérsékleten.
(beadási határidõ:
Március 11.)
8.: feladat: Atkins:
Gyakorlatok 20.18
Határozza meg a I2(g)
= 2I(g) reakció egyensúlyi állandóját
1000 K hõmérsékleten, a I2-molekula következõ
adataiból: 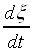 = 214,36
cm-1; B = 0,0373 cm-1;
De = 1,5422 eV.
= 214,36
cm-1; B = 0,0373 cm-1;
De = 1,5422 eV.
(beadási határidõ:
Március 11.)
9.: feladat:
Számítsa ki a 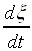 reakciósebességet a
reakciósebességet a  alapján, és mutassa meg, mikor arányos
alapján, és mutassa meg, mikor arányos 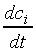 a reakciósebességgel.
a reakciósebességgel.
(beadási határidõ:
Március 25.)
10.: feladat:
Oldja meg a parciális törtekre bontás módszerével
a 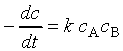 differenciálegyenletet, ha
differenciálegyenletet, ha 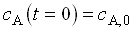 és
és 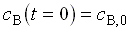 .
(Explicit megoldást kérünk beadni.)
.
(Explicit megoldást kérünk beadni.)
(beadási határidõ:
Március 25.)
11.: feladat:
Írjon fel 10 db elemi reakciót, ami lejátszódhat
a metán égése során, és sorolja be mindegyiket
a láncreakcióban játszott szerepe szerint.
(beadási határidõ:
Április 8.)
12.: feladat:
Igazolja, hogy a
C2H6 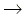 C2H4
+ H2
C2H4
+ H2
reakció elsõrendû az alábbi értelemben:
ha a következõ mechanizmus szerint játszódik
le:
Fontos! Az elsõ reakciót bimolekulásnak (másodrendûnek)
tekintse. Mindhárom gyököt tekintse kvázistacionárius
komponensnek. Adja meg a fentiek alapján a k kifejezését
is.
(beadási határidõ:
Április 8.)
13.: feladat:
Adja meg az 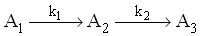 két, sorbakapcsolt
unimolekulás elemi lépésbõl álló
mechanizmus c1(t), c2(t)
és c3(t) megoldásfüggvényét
a c1(t = 0) = c1,0 és
c2(t = 0) = c3(t = 0)
= 0 kezdeti feltételek mellett. A számításokat
sajátérték-sajátvektor módszerrel végezze.
Vázolja grafikusan a megoldásfüggvényeket. Plusz
pont jár a megoldás ellenõrzéséért.
két, sorbakapcsolt
unimolekulás elemi lépésbõl álló
mechanizmus c1(t), c2(t)
és c3(t) megoldásfüggvényét
a c1(t = 0) = c1,0 és
c2(t = 0) = c3(t = 0)
= 0 kezdeti feltételek mellett. A számításokat
sajátérték-sajátvektor módszerrel végezze.
Vázolja grafikusan a megoldásfüggvényeket. Plusz
pont jár a megoldás ellenõrzéséért.
(beadási határidõ:
Április 22.)
14.: feladat:
A CH4 + OH 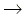 CH3
+ H2O hõmérsékletfüggésének
ábrázolása 20oC -
80oC és 20oC
- 2500oC hõmérséklettartományban.
A kiterjesztett Arrhenius együtthatók átszámítása
kétparaméteres Arrhenius kifejezéssé a szûkebb
hõmérséklettartományban.
CH3
+ H2O hõmérsékletfüggésének
ábrázolása 20oC -
80oC és 20oC
- 2500oC hõmérséklettartományban.
A kiterjesztett Arrhenius együtthatók átszámítása
kétparaméteres Arrhenius kifejezéssé a szûkebb
hõmérséklettartományban.
(beadási határidõ:
Április 22.)
A tanszék web-lapjai : http://www-PhCh.chem.elte.hu
Utolsó módosítás: 1999.
április 13.
.Webmaster:
Tunyogi Helga
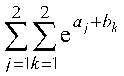 szorzatösszeget.
szorzatösszeget.
 alapján, és mutassa meg, mikor arányos
alapján, és mutassa meg, mikor arányos 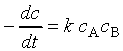 differenciálegyenletet, ha
differenciálegyenletet, ha C2H4
+ H2