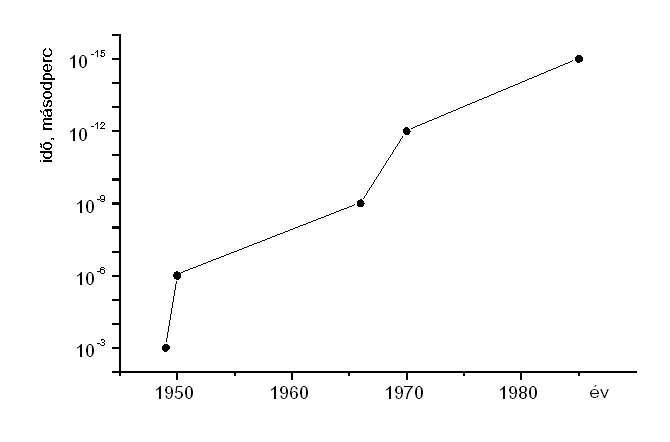
1. ábra Az idõfelbontás alakulása a reakciókinetikában az utóbbi 40 év során.
(kivonat Keszei Ernõ „Femtokémia"
címû monográfiájából:
A kémia újabb eredményei 86. kötet, Akadémiai
Kiadó Budapest, 1999)
Megnézhetõ a 3.1. alfejezet 6. ábráján bemutatott berendezés mûködõ változata is!
A femtokémia vagy más néven ultragyors jelenségek kémiája a 80-as évek végén elért femotszekundum (1fs = 10-15 s) idõfelbontásról kapta a nevét. Az elnevezés Ahmed H. Zewail-tól származik, aki 1987-ben elõször közölt kísérleti eredményeket átmeneti komplex (transition state) fluoreszcenciaspektrumának detektálásáról [1]. Ebben a közleményben még FTS-nek (Femtosecond Transition-state Spectroscopy) nevezi a módszert, de 1988-ban írt két összefoglaló cikkének címe [2,3] már „Laser Femtochemistry", ami újabb egy év után „Femtochemistry"-re rövidült [4]. Az elsõ ilyen néven meghirdetett konferenciát 1993 márciusában tartották Berlinben, 250 résztvevõvel [5]. Ez a konferencia azóta rendszeressé vált. A tudományterület egyéb konferenciákon is képviselteti magát, 1988 óta jelen van pl. a sokkal régebbi „Ultrafast Phenomena" konferenciákon önálló szekcióként.
Nem ez az egyedüli tudományterület, amely nevét a mértékegységek körében használt elõtagról kapta. Ha eltekintünk pl. a mikroeletkronika kifejezéstõl, amiben a mikro elõtag inkább kis méretre, mint m-re vagy A-re utal, az utóbbi évtizedben kialakult nanoszerkezet szó is ebbe a csoportba tartozik, amelyben a nano elõtag egyértelmûen a nm hosszúságegységbõl származtatható. A femtokémia szó ugyan egy femtoszekundum körüli idõtartamot sugall, de nem egy vagy néhány, hanem inkább 10, sõt 100 fs nagyságrendû idõintervallumokat kell alatta érteni. A kifejezést a napjainkban egyre divatosabbá váló rekordhajsza szülte, de nem véletlen, hogy éppen az idõfelbontás területén. A reakciókinetika történetének végigkövetésével beláthatjuk, hogy az itt elért idõfelbontásban valóban meglehetõsen egyedülálló „sportteljesítménynek" lehettünk tanúi.
A reakciókinetika tudományos igényû mûvelésének elsõ eredménye Wilhelmy nevéhez fûzõdik, aki 1850-ben írta fel a nádcukor inverziójára az azóta másodrendû sebességi egyenletnek nevezett differenciálegyenletet. Az általa tanulmányozott, reakció percekben kifejezhetõ idõk alatt játszódott le. A századfordulón Rutherford által gázreakciók vizsgálatára kifejlesztett, majd 1940-ben Chance által megállított áramlásos módszerként folyadékokra is sikerrel alkalmazott áramlásos módszerekkel a tanulmányozható reakcióidõt le lehetett csökkenteni néhány ms-ig, de nem tovább. A reakciókinetika elsõ 100 évét tehát négy nagyságrendnyi idõskála-rövidülés jellemezte. A további rövidülés legfõbb akadálya az volt, hogy a rekacióelegyet ms-nál rövidebb idõ alatt nem lehetett összekeverni.
Az áttörést ezért az az ötlet jelentette, amellyel ki lehetett küszöbölni a reakcióelegy összekeverését reakcióképes állapotban. A keverést úgy végezték el, hogy a homogén elegyben ne történjen reakció, majd ezután egy hirtelen, nagyon gyors beavatkozással elindították a reakciót. Ennek az ötletnek a megvalósítása késõbb (1967-ben) Nobel-díjat ért a villanófény-fotolízis kifejlesztõinek, Norrish-nak és Porter-nek, illetve a relaxációs módszerek kifejlesztõjének, Eigennek.
Az „idõrekord" további növelése szempontjából a villanófény-fotolízis bizonyult perspektivikusnak. Az 1. ábrán látható, milyen ütemben fejlõdött a módszer idõfelbontása. A reakciókinetika elsõ évszázadának négy nagyságrendet átfogó felbontásnövekedése után az azt

követõ negyven év 11 nagyságrend felbontásnövekedést eredményezett. Ez valóban olyan egyedülálló „csúcsteljesítmény" a természettudományokban, ami érthetõbbé teszi a fellengzõsen hangzó femtokémia kifejezést.
Érdemes megvizsgálni még két kérdéskört. Az egyik az, hogy hol helyezkedik el a fizikai jelentéssel bíró idõ skáláján a 10 fs, és annak milyen konkrét folyamatok felelnek meg. A másik az, hogy vajon meddig lehet vagy érdemes törekedni a még nagyobb idõfelbontásra. A fizikai modellekben elõforduló legrövidebb idõ 10-40 s nagyságrendû, és az univerzum keletkezésével, az õsrobbanással kapcsolatos. A Földön jelenleg kísérletileg is hozzáférhetõ idõk ennél lényegesen hosszabbak. A nukleonok atommagbeli mozgásának karakterisztikus ideje 10-20 másodpercre becsülhetõ. A kémiai folyamatok közül a leggyorsabb az elektronszerkezet átrendezõdése (pl. fotongerjesztést követõen), amelynek ideje kb. 0,1 fs. A neutrinótávcsövek korában azonban nem feledkezhetünk meg az olyan - eredményükben kémiai - folyamatokról sem, amelyek a molekulán áthaladó igen nagy energiájú fotonok vagy neutrinók és molekulák, illetve az atommagok kölcsönhatásának eredményei. Ezek karakterisztikus ideje a részecskéknek a molekulán (átmérõ kb. 300 pm), illetve az atommagokon (átmérõ kb. 3 fm) történõ áthaladási idejébõl számítható. Ebbõl molekulák esetére kb. 1 as (1 attoszekundum = 10-18 s), atommagok esetére pedig kb. 10 ys (1 yoctoszekundum = 10-24 s) adódik. Azt mondhatjuk tehát, hogy a kísérletileg érdekes és szóbajöhetõ idõskálából még 9 nagyságrend „meghódítása" hátra van.
2. ábra A fizikában és a kémiában értelmezhetõ idõtartamok vázlata, valamint a fontosabb molekuláris események idõskálája.
Ha a klasszikus értelemben vett,
kipreparálható termékekhez vezetõ kémiai
reakciókat tekintjük, azok végbemenetele az atommagok
szerkezetének átrendezõdésével jár.
Ennek idõskálája a molekularezgések karakterisztikus
idejének nagyságrendjébe esik, ami a kemény
rezgések esetén (pl. C-H vagy O-H nyújtás)
10 fs körül van, míg lágyabb rezgések esetén
elérheti a 100 fs-ot, sõt, deformációs rezgések
részvételekor ennél is hosszabb lehet. Ezek az idõk
az ultragyors lézerfotolízis jelenlegi módszereivel
már mérhetõk. Nagyon sok reakció szempontjából
fontos, sebességmeghatározó folyamat a rezgési
energia redisztribúciója a molekulán belül, ami
gyakran 1 ps vagy annál rövidebb idõ alatt játszódik
le, de elõfordulhat az is, hogy ez az idõ kiterjed a nanoszekundumok
tartományáig, különösen ha a forgási
energiák redisztribúcióját is magában
foglalja. Az oldószerekben lejátszódó reakciók
egyik nagyon fontos részfolyamata a szolvatáció (oldószer-relaxáció)
ami jellegzetesen pikoszekundum körüli idõtartományban
megy végbe. A kémiai reakciókban megjelenõ
további folyamatok már nem tartoznak az ultragyors reakciók
csoportjába. A pikoszekundum és nanoszekundum közötti
idõtartományban már megjelenik a diffúzió,
valamint a molekulák ütközése is. Ezek sebességét
már nem annyira ez elemi molekuláris folyamatok sebessége,
mint inkább statisztikai faktorok határozzák meg.
2. Ultragyors lézerek
2.1. A lézerek
mûködésének alapjai
A lézer az angol Light Amplification by Stimulated Emission of Radiation kifejezésbõl alkotott „laser" mozaikszó hangutánzó magyar átírása. Az elnevezés elárulja a lézermûködés alapvetõ mozzanatát, az indukált fénykibocsátást. Ha valamely átlátszó anyagi közegben vannak olyan atomok vagy molekulák, amelyeknek két energiaszintje közötti energiakülönbség éppen megfelel egy olyan foton energiájának, amit a kisebb energiájú állapot elnyelni, a nagyobb energiájú állapot pedig kibocsátani képes, akkor egy ilyen foton indukálja a nagyobb energiájú állapot átmenetét a kisebb energiájú állapotba, melynek során az indukáló fotonnal azonos tulajdonságú: azonos hullámhosszú, irányú és fázisú foton bocsátódik ki. Ugyanezt a fotont azonban a kisebb energiájú állapotban lévõ atom vagy molekula el is nyelheti. A lézer mûködéséhez ezért arra van szükség, hogy a fénykibocsátó nagyobb energiájú állapot betöltöttsége nagyobb legyen, mint a fényelnyelõ kisebb energiájú állapoté. Azt a hullámhossztartományt, amelyben a fénykibocsátás mértéke nagyobb, mint a fényelnyelésé, a lézer erõsítési sávjának nevezzük. Ezen a sávon kívül esõ hullámhosszakon a lézer veszteséges.
A fényerõsítés hatásfoka jelentõsen növelhetõ, ha ugyanaz a foton többször is áthaladhat az erõsítõ közegen, hiszen minden áthaladás során kiválthat újabb fénykibocsátást. Az erõsítõk leírására használt szaknyelvben ezt visszacsatolásnak nevezik. A lézerek fontos alkotórésze ezért az ún. rezonátorüreg, amit a berendezés két végén elhelyezett tükrök határolnak. Ezeket a tükröket úgy kell beállítani, hogy a közöttük fellépõ interferencia az erõsítési sávban lévõ megfelelõ hullámhosszra nézve erõsítõ (konstruktív) interferencia legyen.
Tekintsük át, hogyan játszódik le a fényerõsítés a rezonátorüreg két tükre közé helyezett erõsítõ közegben. Az erõsítõben mindenekelõtt azt kell biztosítani, hogy a lézermûködést lehetõvé tevõ energiaszintek közül a magasabb szint betöltöttsége nagyobb legyen, mint az alacsonyabbé. Tudjuk, hogy ez általában nem így van, hiszen a molekuláris energiaszintek betöltöttsége Boltzmann-eloszlást követ, amely szerint az energia növekedésével az energiaszintek betöltöttsége exponenciálisan csökken. A lézermûködéshez ennek a betöltöttségnek a megfordítására, latin eredetû szóval populációinverzióra van szükség. Ennek elérését, illetve fenntartását a magasabb szintre történõ szivattyúzással, holland eredetû szóval pumpálással végzik, amit különbözõ módszerekkel lehet megvalósítani. Ha a rezonátorüregben pumpálással fenntartják a populációinverziót, akkor a magasabb energiaszintû állapotok véletlenszerûen, spontán is bocsátanak ki fotonokat. Ezek a fotonok további fotonok kisugárzását indukálják, és ha irányuk éppen olyan, hogy a rezonátorüreg tükrei között oda-vissza verõdnek, akkor minden egyes áthaladás során további fotonok kisugárzását indukálják, amelyek velük megegyezõ hullámhosszúak, irányúak és fázisúak. Ha gondoskodnak a folyamatos pumpálásról, akkor egyre több energia koncentrálódik a rezonátorüregben, koherens fotonok formájában. Ez az energiaforrás úgy „csapolható meg", ha a rezonátorüreg egyik végén lévõ tükör részben áteresztõ. Ekkor a keletkezõ fotonok adott hányada folyamatosan kiléphet a rezonátorüregbõl. Ezt a kilépõ párhuzamos, monokromatikus és koherens sugárzást nevezzük lézersugárzásnak.
A lézerek mûködésének alapjairól magyar nyelven jó összefoglaló olvasható Atkins „Fizikai kémia" címû tankönyvében [6], valamint részletesebben Csillag és Kroó kismonográfiájában [7], ami könyvtárakban megtalálható.
2.2. Az impulzuslézerek mûködésének elve
Mûködõ lézerek tervezéséhez a fentieken túlmenõen egy sor technikai részletet kell figyelembe venni. A rezonátorüregben az interferencia következtében állóhullámok alakulnak ki, amelyek intenzitásprofiljának az üreg tengelyére merõleges komponense csak olyan lehet, amilyent a rezonanciafeltétel megenged. Az ennek megfelelõ intenzitásprofilokat a lézer transzverzális módusainak nevezik. A rezonátorüreg L hosszúsága az erõsített fény hullámhosszára nézve is szigorú feltételeket szab. Konstruktív interferencia csak akkor lép fel, ha az üreg L hossza a fény l/ 2 félhullámhosszának N egész számú többszöröse, más hullámhosszaknál az interferencia következménye kioltás, ami az erõsítést meghaladó rezonátor-veszteséget, azaz a lézerhatás megszûnését vonja maga után. Ez a lézer által erõsített fény hullámhosszára a
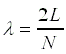
feltételt írja elõ, amit a n frekvenciára
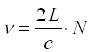
alakban írhatunk fel, ahol c a fény terjedési sebessége az üregben. A rezonátorüreg által erõsített fény frekvenciája tehát a 2 L /c hányados egész számú többszöröse lehet. Az ennek megfelelõ frekvenciákat a lézer longitudinális módusainak nevezzük. A longitudinális módusok közül természetesen csak az jöhet szóba a lézer erõsítése szempontjából, amelyik pontosan megfelel az erõsítõ közeg két energiaszintje közötti átmenetnek. Ha az erõsítõ közeg gáz vagy szilárd anyag, akkor általában csak egy vagy néhány, pontosan meghatározott energiaátmenet lehetséges. Ilyenkor a rezonátorüreg tükreit az adott frekvenciának megfelelõ távolságra kell beállítani. Ha az erõsítõ közeg alkalmas festék folyékony oldata, akkor abban az erõsítési sáv nagyon széles, gyakran több mint 100 nm hullámhossztartományra kiterjedõ is lehet. Mivel ezeknek a festéklézereknek a hullámhossza így megfelelõ beállítással széles határok között változtatható, ezeket szokás hangolható lézereknek is nevezni.
A hangolás azonban további problémákat is felvet. A széles erõsítési sávban sok különbözõ frekvencia kielégíti a 2.2 egyenletet, ezért a kibocsátott lézerfény nem lenne monokromatikus, ha ezt külön nem biztosítanák. A hangolható lézerekbe ezért még egy hangoló egységet is beépítenek. Ez célszerûen pl. egy optikai rács vagy prizma, amely a rezonátorüreg tengelyével bezárt szögtõl függõen tengelyirányban csak adott hullámhosszúságú fényt enged át, ezért így a lézer csak ezt a fényt erõsíti. Az eddigieket összefoglalva azt mondhatjuk, hogy a lézerek alapvetõen fontos elemei a rezonátorüreg két (finoman pozícionálható) tükre, az erõsítõ közeg, valamint a pumpáló és a hangoló egység. Mivel jelen alfejezet célja az impulzuslézerek mûködési alapjainak áttekintése, vegyük szemügyre a lézerekben kialakuló fényimpulzusok tulajdonságait.
3. ábra. Lézerberendezés vázlatos rajza.
A jól hangolt, folyamatosan pumpált lézerekben a hangolásnak megfelelõ hullámhosszú fény a rezonátorüreg által fenntartott transzverzális módusú hullámcsomagok formájában koncentrálódva alakul ki, erõsödik fel, és hagyja el a lézerüreget a részben áteresztõ tükrön keresztül. A különbözõ módusú, ezen belül is különbözõ fázisú hullámcsomagok véletlenszerûen alakulnak ki és hagyják el a lézerüreget. Ennek következményeként a lézerbõl kilépõ fény intenzitása idõben ingadozik, de átlagos teljesítménye állandó. Arra is van lehetõség, hogy a lézer különbözõ longitudinális módusainak fázisát szinkronizáljuk, El lehet érni, hogy csak a transzverzális alapmódus alakuljon ki a rezonátorüregben, és egyszerre csak egy ilyen - Gauss-profilú - impulzus haladjon át az üregen. Az ilyen módusszinkronizált (angolul mode-locked) lézer egy olyan impulzus-sorozatot bocsát ki, amelyben a csúcsokat egymástól a rezonátorüreg teljes L hosszának kétszerese (a fényút a részben áteresztõ tükörtõl a másik tükörig és vissza) választja el, ami idõben éppen 2L / c. (Ennek reciprokát nevezzük a lézer ismétlési frekvenciájának.) A rezonancia-feltételek alapján az is kiszámítható, hogy az egyes csúcsok idõbeli szélessége a lézer erõsítési sávszélességének a reciproka, azaz 1/Dn.
A módusszinkronizáció többféle módszerrel elérhetõ. Aktív módusszinkronizációnak azt nevezik, amikor a rezonátorüregben egy fényszaggatót mûködtetnek külsõ meghajtóval. Ez a fényszaggató csak 2L / c idõnként nyitja ki a fényutat, egyébként zárva tartja, emiatt a lézer csak azt a hullámcsomagot (impulzust) erõsíti, amely pontosan a nyitás pillanatában ér a szaggatóba. Ez pl. megvalósítható olyan kristállyal, amely feszültség hatására igen gyorsan megváltoztatja fényáteresztõ képességét. Ha erre a kristályra olyan frekvenciájú váltakozó feszültségjelet kapcsolunk, amely pontosan megfelel a 2L / c ismétlési frekvenciának, akkor az éppen a módusszinkronizációhoz szükséges ütemben változtatja a rezonátorüreg erõsítését. Ezt a módszert nevezik Q-kapcsolásnak. Az elnevezés a rezgõkörök rezonanciatulajdonságainak „jóságát" kifejezõ Q-tényezõ analógiájára született. (A Q-kapcsolás nemcsak a 2 L /c ismétlési frekvenciájú, hanem annál sokkal ritkább impulzusok elõállítására is alkalmazható.)
A módusszinkronizálás másik aktív módja a szinkron pumpálás. Ennek során egy meghajtó impulzuslézer pumpálja a szóbanforgó lézert, ezért a meghajtott lézer erõsítése csak akkor lépi túl a veszteségeket, amikor a meghajtó impulzus annak erõsítõ közegében kiváltja a populációinverziót. Ez az elrendezés azt eredményezi, hogy a meghajtott lézer (általában festéklézer) impulzusai sokkal rövidebbek lesznek, mintha pl. Q-kapcsolással szinkronizálnánk. Nagyon fontos a két lézer rezonátorüregének pontos összehangolása, különben ez a módszer nem mûködik. Ez azt jelenti, hogy a meghajtott lézer hosszának egész számú többszöröse legyen a meghajtó lézer hossza.
A passzív módusszinkronizálás nem külsõ beavatkozással történik, hanem a lézer mûködése közben önmagától bekövetkezik. A jelenséget pl. a rezonátorüregben elhelyezett telíthetõ fényelnyelõ festékkel lehet kiváltani. Ez a festék besugárzás nélkül színes, azaz erõsen abszorbeál, a lézerfény abszorpciója során viszont átlátszóvá válik. Ha a festéken áthaladó fényimpulzus elegendõen nagy intenzitású, akkor annak egy része telíti az abszorpciót, amitõl a festék átlátszóvá válik, és átereszti az impulzust. Az abszorbeáló festék és az erõsítõ válaszidejétõl függõen kétféle mûködési módja van a passzívan módusszinkronizált lézereknek.
Az egyik mód „ritka impulzusok" (angolul „burst mode") elõállítását teszi lehetõvé. Ebben az esetben az erõsítõ magasabb energiaszintje hosszú, akár néhány száz mikroszekundum élettartamú. Ehhez képest a lézerimpulzus nagyon rövid idejû. A pumpáló villanófény hatására betöltõdõ magasabb energiaszint kezdetben spontán emisszióval elindít fotonokat, amelyek indukált emissziót kiváltva számos különbözõ fázisú lézerimpulzust hoznak létre a rezonátorüregben. Ezek a módusok fluktuációjuk során különbözõképpen erõsítõdnek. Ha valamelyik közülük eléri azt az erõsítést, amely képes telíteni a fényelnyelõ festéket, akkor az azon sokkal kisebb veszteséggel halad át, mint a kisebb intenzitású módusok, ezért azoknál jobban erõsödik, így nagyon hamar ez lesz az uralkodó impulzus egészen addig, amíg annyira felerõsödik, hogy az erõsítõ közeg anyagával erõs nemlineáris optikai kölcsönhatás során idõben szétesik, így az abszorbeálódó festéket nem tudja már terjedésével szinkronban modulálni. Ekkor a véletlen fluktuációkból újabb impulzus kiválasztására és felerõsítésére nyílik lehetõség. A „ritka impulzusú" lézerek impulzusszélességét a fényelnyelõ festék átlátszó gerjesztett állapotának élettartama korlátozza. A használatos festékek élettartama néhány pikoszekundum nagyságrendbe esik. Ezzel a módszerrel mûködik pl. a módusszinkronizált rubinlézer, vagy a neodímium-üveg lézerek. Az impulzusok sûrûségét általában Q-kapcsolással szabályozzák.
4. ábra. Telíthetõ festék (abszorber) segítségével passzívan móduslokalizált lézer vázlata.
A másik módszer a folyamatos
vagy kvázi-folyamatos lézerek módusszinkronizálása.
Ezekben a módusszinkronizált impulzusok sokkal rövidebbek,
mint akár a fényelnyelõ festék, akár
az erõsítõ gerjesztett állapotának idõtartama.
Ilyen körülmények között jó közelítéssel
hiperbolikus szinuszfüggvény profilú impulzusok alakulnak
ki. Az impulzus két „farka" a rezonátorüregben megtett
oda-vissza út során a veszteségek következtében
gyengítõdik, míg az impulzus csúcsa eközben
erõsödik, azaz ennek eredõjeként az impulzus
szélessége csökken. Ennek az a feltétele, hogy
az erõsítõ közeg magasabb energiaszintjének
élettartama azonos nagyságrendû legyen, mint a rezonátorüregben
az oda-vissza út megtételéhez szükséges
idõ (az ún. körülfutási idõ),
az abszorpció hatáskeresztmetszete pedig több mint kétszerese
legyen az erõsítés hatáskeresztmetszetének.
Ilyen körülmények között a fényelnyelõ
festék hamarabb telítõdik (és átlátszóvá
válik) mint az erõsítõ. Az impulzus elöl
haladó „farkát" gyengíti a még nem telített
abszorpció, az impulzus csúcsa viszont kiüríti
az erõsítõ magasabb energiaszintjét, így
annak a csúcs mögötti „farka" nem erõsödik.
Az impulzus addig „karcsúsodik" és erõsödik,
ameddig fenn tudja tartani azt a feltételt, hogy a fényelnyelõ
festék elõbb telítõdik, mint amikorra az erõsítõ
elveszíti gerjesztettségét.
2.3. Pikoszekundumnál
rövidebb lézerimpulzusok elõállítása
Az elsõ nagyenergiájú,
pikoszekundumnál rövidebb lézerimpulzust Shank és
Ippen állította elõ 1974-ben [8], passzívan
módusszinkronizált festéklézerrel. A következõ
jelentõs lépés az ütközõ impulzusokkal
módusszinkronizált (angolul colliding pulse mode-locked,
rövidítve CPM) lézer kifejlesztése volt 1981-ben
[9], amellyel 100 fs-nál valamivel rövidebb impulzusokat állítottak
elõ. A CPM lézerben két, egymással
szemben haladó impulzus a telíthetõ fényelnyelõben
találkozik („ütközik"), így a két impulzusra
nézve kisebb az elnyelés telítésére
fordított veszteség. Emiatt a festék elnyelése
növelhetõ, aminek eredményeképpen keskenyebb
impulzusok alakulnak ki. Az impulzusütköztetésnek nagyon
pontosnak kell lennie, ha egyenes rezonátorüregben akarjuk
a lézert mûködtetni. Ez az érzékenység
kiküszöbölhetõ, ha a rezonátorüreg nem
egyenes, hanem „gyûrût" képez (3. ábra).
A gyûrûben egymással szemben haladó impulzusok
automatikusan szinkronizálódnak.
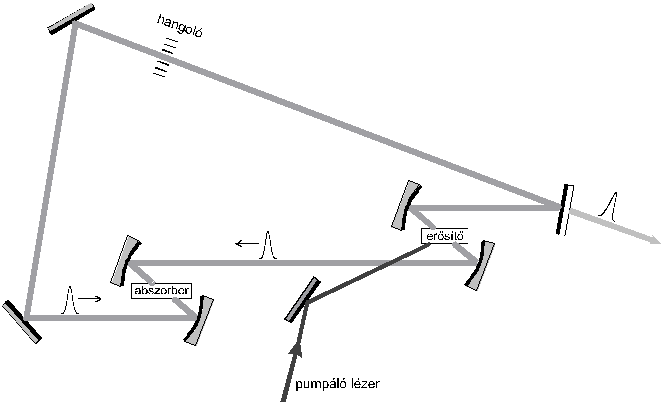
5. ábra. Gyûrûs elrendezésû CPM festéklézer felépítése.
A gyûrûs elrendezésû CPM festéklézereket a 80-as évek végén már kereskedelmi forgalomban is lehetett kapni, és segítségükkel 20-50 fs szélességû impulzusokat lehetett elõállítani. Ehhez még szükség volt a törésmutató diszperzió következményeként fellépõ csoportsebesség-diszperzió kompenzálására, hogy a spektrális sávszélesség miatt fellépõ impulzus-kiszélesedést megakadályozzák. Ez a diszperziót „visszakomprimáló" prizmákkal vagy optikai rácsokkal érhetõ el. A lézerek kémiai alkalmazásához olyan teljesítményre van szükség, amely elegendõ mérhetõ mennyiségû változás elõidézésére. Mivel az ultragyors lézerek impulzusai igen rövidek, energiájuk általában csak nanojoule nagyságrendû. Kémiai alkalmazásuk elõtt ezeket az impulzusokat még tovább kell erõsíteni. Az optikai pumpálással mûködõ festéklézerek képesek erre az impulzuserõsítésre. Az egyik legnagyobb technikai probléma eközben a nagy erõsítésû közegben spontán keletkezõ „zajimpulzusok" erõsödésének megakadályozása. A leggyakoribb megoldás egy többfokozatú erõsítõben a fokozatok közé elhelyezett telíthetõ fényelnyelõ festék, ami meggátolja a zaj erõsítését. Az erõsítõ a következõképpen mûködik. Az impulzus fényútja mentén egymás után elhelyeznek néhány festékcellát, közéjük pedig abszorbeáló festéksugarat, amelybe belefókuszálják az áthaladó lézerfényt. Az erõsítõ festékcellákat egy impulzuslézerrel pumpálják, amelynek sugarát úgy osztják meg, hogy minden erõsítõ cellára kb. azonos fényáram essen. Az erõsítõ festék gerjesztett állapotának élettartama kb. megegyezik a pumpáló impulzus hosszával. Amikor a gerjesztett festéken az erõsítendõ impulzus áthalad, „kisöpri" a populációinverziót, amitõl felerõsödik. 3-4 fokozatú erõsítõvel így 103-104-szeres erõsítés érhetõ fel. A festékoldatokon áthaladva az impulzus a törésmutató diszperziója következtében kiszélesedik, ezért a kimenõ impulzust prizmákkal vagy rácspárral még újra összenyomják, mielõtt alkalmazásra kerül.
Ezzel a módszerrel a nanojoule nagyságrendû energia 100 J nagyságrendûre erõsíthetõ. Ha ekkora energiatartalma van egy 100 fs szélességû impulzusnak, akkor a teljesítménye 1000 GW, amely már elegendõ jól detektálható kémiai változás elõidézésére.
Az impulzus kiszélesedését az erõsítõben hasznosítani is lehet. Ha egy 10 fs szélességû impulzus 1 mm vastag üvegen halad át, akkor közel kétszeresére szélesedik ki. Ez a kiszélesedés olyan, hogy a gyorsabb vörös felõli hullámhosszak elõresietnek, a lassúbb kék felõli hullámhosszak pedig lemaradnak. A szélesebb impulzus nagyobb hatásfokkal erõsíthetõ, majd egy párhuzamos fényvisszaverõ rácspár segítségével újra összenyomható. A rácsok távolságának alkalmas beállításával érhetõ el a megfelelõ mértékû impulzus-összenyomás. Az impulzus-összenyomás módszerével sikerült elõször elõállítani a legrövidebb impulzusokat is. Rácspárok és prizmák alkalmazásával 1986-ban 6 fs szélességû impulzust állítottak elõ [10].
Az eddig leírt ultragyors lézerimpulzus-elõállítási módszerek módusszinkronizált festéklézerek alkalmazására épültek. Ezek nagy hátránya viszonylag kis stabilitásuk, és a festékoldatok nehézkes kezelése. Részben emiatt számos más erõsítõközeggel, más elveken mûködõ lézert is kifejlesztettek ultragyors impulzusok elõállítására. Egyik nagy alkalmazási területükön, az optikai távközlésben pl. a több száz GHz frekvenciával stabilan mûködõ ultragyors lézerdiódák is jól alkalmazhatók, mert az optikai kábelekben elegendõ néhány watt teljesítményû impulzusok használata is. A nagyteljesítményû lézerek között a festéklézerek mellett leginkább a Ti: zafír (erõsítõ közegként titánnal szennyezett zafírt alkalmazó) szilárdtestlézer terjedt el [11]. A titánnal szennyezett zafír erõsítõ sávszélessége 790 nm környékén mintegy száz nanométer, amin belül bárhova hangolható. A festéklézerekhez hasonlóan mûködtethetõ kvázifolytonos módusszinkronizált üzemben, nagy ismétlési frekvenciával. Stabilitása sokkal nagyobb mint a festéklézereké, és egy ilyen berendezést már egy vegyész is képes mûködtetni (az optikusok általában „felhasználóbarátnak" nevezik a könnyebben kezelhetõ lézereket.). A Ti: zafír szilárdtestlézer ára is kedvezõbb, egy ultragyors festéklézer árának egyre csökkenõ hányada.
A stabil impulzusokat elõállítani képes módusszinkronizált festéklézereket szokás „második generációs" lézereknek is nevezni. A kisülési lámpával vagy gázlézerekkel pumpált ultragyors módusszinkronizált szilárdtestlézerek alkotják a „harmadik generációt", míg a jelenleg még kifejlesztés alatt álló, csak diódalézerrel pumpált módusszinkronizált ultragyors lézerek alkotják (majd) a negyedik generációt. A lézerek árának jelentõs csökkenése várható, ha a pumpáló lézert sikerül egy egyszerû diódalézerrel felváltani.
Több szilárdtestlézerrel sikerült megvalósítani az ún. „optikaiKerr-lencsés " módusszinkronizációt. Ennek alapja az, hogy a lézer szilárdtest erõsítõje a rajta áthaladó nagyintenzitású lézerimpulzus hatására a fény intenzitásával arányos additív taggal növeli a törésmutatóját. Megfelelõ optikai tervezés esetén ez a jelenség hasonló amplitúdómodulációt okoz, mint a telíthetõ festékek. Az óriási különbség az, hogy ennek az optikai Kerr-effektusnak a kapcsolási ideje 1-2 fs nagyságrendû, ezért megfelelõ elrendezés esetén mindössze egy ilyen passzív Kerr-elem hatására néhány femtoszekundum szélességû impulzusokat lehet elõállítani. Az eddig ismert legrövidebb impulzusokat (6-8 fs) is Kerr-lencsével módusszinkronizált Ti : zafír lézerrel sikerült elõállítani [17,18].
2.4. Idõmérés a pikoszekundumnál rövidebb tartományban
Az ultragyors lézerek alkalmazása alapvetõen kétféle idõmérési problémát vet fel. Az egyik probléma az impulzusok idõbeli kiterjedtségének (szélességének és alakjának) meghatározása, a másik pedig a lézerimpulzusok segítségével végzett mérések során eltelt - nyilván az impulzusszélességgel összemérhetõ tartamú - idõ mérése. Ilyen rövid idõk mérésére természetesen szóba sem jöhet fényérzékelõ elektronikus berendezések és oszcilloszkóp használata, hiszen a GHz körüli maximális mûködési frekvencia az elektronikus berendezések válaszidejét nanoszekundum nagyságrendûre korlátozza.
Az idõmérést gyakran távolság mérésére vezetjük vissza. Ez történik az ultragyors idõmérés esetében is, amelynek két alapvetõen különbözõ módszere alakult ki. Az egyiket szokás kronoszkópiának is nevezni, a mérésre használt berendezés angol neve pedig a streak camera [12]. Ennek alapelve egy fotokatódon igen gyorsan képzõdött fotoelektronok igen nagymértékû gyorsítása és eltérítése, majd azok megjelenítése egy foszforeszkáló ernyõn - amit azután le is lehet fényképezni, vagy fényérzékelõ digitális jelfeldolgozóval megjeleníteni. A nagy eltérítõfeszültség lehetõvé teszi a gyors eltérítést; az írás sebessége általában néhányszor 1010 cm/s, azaz 0.1 mm távolság a pikoszekundum törtrészeit jelenti. A fényképen vagy a digitálisan feldolgozott jelen az eltérülési távolság az idõvel, a feketedés vagy jelintenzitás pedig a fényintenzitással arányos. A streak camera elõnye, hogy segítségével kellõ fényerõsítés esetén egyetlen impulzusból is meghatározhatunk akár impulzusalakot, akár valamely tanulmányozott folyamatban idõfüggõ fényintenzitást, és mindezt - legalábbis elvileg - lineáris idõ- és intenzitás-skálán. Hátránya azonban a viszonylag magas ár és a kis érzékenység, továbbá a korlátozott idõfelbontás. Vannak azonban olyan jelenségek, amelyek természetüknél fogva csak egyetlen impulzus alatt jelentkeznek, és nem ismétlõdnek impulzusról impulzusra. Ilyenek pl. az ingadozási jelenségek, amelyeknek mérésére a streak camera alkalmazható a legcélszerûbben. Idõ- és intezitásskálája egyszerûen kalibrálható, ha két szembelévõ tükör közé egy lézerimpulzust bocsátanak, amelynek egy része oda-vissza reflektálódik, nem reflektált része pedig a streak camera bemenõ résére jut. A kamerában megjelenõ impulzusok közti idõ a tükrök L távolságától függõen 2L / c, az egymást követõ impulzusok intenzitása pedig a két tükör reflektivitásának R1·R2 szorzata.
Az idõmérés másik módszere két impulzusnak egymáshoz képest változtatható késleltetésén alapszik. Az idõt ebben az esetben a két impulzus közti késleltetés határozza meg, azaz ezzel a módszerrel egy impulzus felhasználásával csak egyetlen idõponthoz tartozó intenzitásadat mérhetõ. A módszer impulzusszélesség és impulzusalak meghatározására csak a nagyenergiájú fényimpulzusok nemlineáris optikai tulajdonságainak felhasználásával alkalmazható.
Ha a fény intenzitása kicsi, akkor a közeg az áthaladó fényre lineáris módon reagál. Az E elektromos térerõsség hatására indukált dipólusmomentum ilyenkor
n = a E (2.3)
Nagy fényintenzitás esetén azonban a közeg válaszfüggvénye már nem lineáris, ami pl. egy hatványsorral írható le:
n = a E + b E2 + g E3 + … (2.4)
Ha a beesõ fény elektromos terét az E = E0 cost függvény írja le, akkor a sorfejtés másodfokú tagjára a
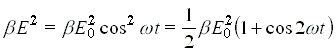
alakot kapjuk, ami a beesõ w körfrekvenciájú fény helyett a 2w körfrekvenciájú, azaz kétszeres frekvenciájú fény kibocsátását teszi lehetõvé. Hasonlóképpen jelentkeznek a magasabb „felhangok" is, egyre kisebb intenzitással. Ezeknek a felhangoknak az elõállítása sokféleképpen lehetséges. Impulzusszélesség meghatározásához legegyszerûbben pl. úgy járnak el, hogy a nagyenergiájú lézerimpulzust egy részben áteresztõ tükörrel kettéosztják, és a két fényimpulzust egy nemlineáris kristályra, pl. káliumdihidrogén-foszfátra (KDP) bocsátják. Megfelelõ körülmények esetén elérhetõ, hogy a kristály csak akkor bocsátja ki a második felharmonikust, ha a két impulzus egyszerre esik a kristályra. A két impulzust egymáshoz képest késleltetve különbözõ mértékû átfedés valósítható meg, és a kibocsátott felharmonikus intenzitása arányos lesz az átfedéssel [13, 14]. Kimutatható, hogy az átfedést leíró integrál éppen a két impulzus alábbi módon értelmezett ún. másodrendû korrelációja:
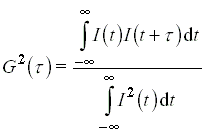
ami a szokásos rövidített írásmóddal a
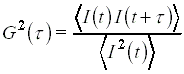
alakban írható fel, ahol
a jel idõszerinti
átlagot jelent, megfelelõen hosszú idõre vonatkoztatva.
Ha a 2.6 kifejezésben az integrálást különbözõ
impulzusalakok esetén elvégezzük, akkor egyrészt
azt tapasztaljuk, hogy a G2(t)
minden esetben szimmetrikus, bármilyen is a kiindulási I(t)
impulzusalak, másrészt a G2(t)
függvény szélessége az impulzus alakjától
függõ mértékben különbözik az
I(t)
impulzus szélességtõl. Az impulzusalak pontos meghatározásához
tehát nem elegendõ egyedül a második felharmonikus
mérése. Kimutatható, hogy ha a másodrendû
korreláció mellett ismerjük a
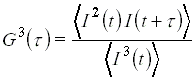
harmadrendû korrelációt is, akkor az impulzusalak, következésképpen az impulzus szélessége is pontosan kiszámítható.
A másodrendû korreláció mérésére kidolgoztak egy olyan módszert is, amely lehetõséget nyújt az impulzusalak meghatározására egyetlen impulzus alapján is. Ez a kétfotonos fluoreszcencia (angolul Two-Photon Fluorescence, TPF) módszere [15, 16], aminek alapja az a jelenség, hogy egy festékoldat adott hullámhosszú fényt nem abszorbeál, csak akkor, ha annak kellõen nagy az intenzitása ahhoz, hogy egyszerre két foton nyelõdjön el, amitõl a festék fluoreszkál. Ha félig áteresztõ tükörrel kettéválasztott fényimpulzus két részét egymással szemben vezetik be egy ilyen festékoldatot tartalmazó küvettába, akkor a beesési irányra merõlegesen az
f (t) = 1 + 2 G2(t) + r1(t) (2.9)
függvény szerint változó fluoreszcencia-intenzitás detektálható. Az r1(t) tag egy idõben igen gyorsan változó függvény, ami a kísérletekben általában nem is látható. A TPF módszer a 2.9 függvény alapján azonban csak olyan impulzusok esetén használható, amelyek idõbeli kiterjedése elegendõen hosszú ahhoz, hogy a fluoreszcenciakép térben kiértékelhetõ felbontást eredményezzen. Ennek alsó határa kb. 1 mm, amit a fény kb. 3 ps idõ alatt tesz meg, a módszer ezért a szub-pikoszekundum idõtartományban már nem alkalmazható.
Az ultragyors lézerek felhasználásával
vizsgált fizikai és kémiai jelenségeknél
az idõmérés általában az adott jelenségtõl
függõ speciális problémákat vet fel. A
megfelelõ idõméréshez fontos az adott rendszer
és az ultragyors lézerimpulzusok kölcsönhatásának
pontos ismerete. Az ilyen jellegû idõméréssel
a késõbbiekben mindig az adott probléma tárgyalásakor
foglalkozunk.
3. Ultragyors kinetikai
mérések
3.1. Egyszerû kétimpulzusos
mérõberendezések
Amint az elõzõ fejezetbõl is kitûnik, pikoszekundumnál lényegesen rövidebb idõk mérésére csak megfelelõen rövid impulzusok közötti idõkésleltetés beállításával van lehetõség. A villanófény fotolízis, illetve a lézerfotolízis esetében ez azt jelenti, hogy a reakciót indító gerjesztõ impulzus (angolul pump) és a reagáló elegy összetételtét mérõ impulzus (angolul probe) közötti idõkülönbség „kódolja" a reakcióidõt. A módszer angol neve ezért pump-and-probe method, ezt nevezzük magyarul egyszerûen kétimpulzusos módszernek. Magyarul ezen kívül használatos a pumpa-szonda kifejezés is, ami a francia pompe-sonde megfelelõje.
Elsõ használata meglehetõsen régi keletû. Porter és Topp alkalmazták 1968-ban, az akkortájt elterjedt nanoszekundumos idõfelbontású Q-kapcsolt rubinlézer forrás segítségével végzett mérésekhez [19]. A gerjesztõ impulzus a rubinlézer kétszerezett frekvenciájú, 347 nm-es impulzusa volt. Mérõ impulzusként az ebbõl részben áteresztõ tükörrel leosztott, késleltetett sugár szolgált, amelyet nagy hatásfokkal és széles sávban fluoreszkáló festékbe fókuszáltak. A fluoreszcencia közelítõleg fehér fényével egy spektrométerben készült fénykép alapján végezték az abszorpciós spektrum detektálását. Minden egyes útkülönbség beállítása után annyit exponáltak, amennyi a kiértékelhetõ feketedéséhez elég volt. Így különbözõ reakcióidõkhöz kaptak egy-egy tranziens spektrumot. A szokásos 1-100 ns idõ 30 cm és 30 m közötti fényútkülönbségek beállítását követelte meg, ami sokszor a laboratórium teljes hosszát többször is átszelõ fényutat jelentett. Az elektronika gyors fejlõdésével a hosszú fényút okozta kényelmetlenséget valós idejû detektálással hamarosan el lehetett kerülni, de a pikoszekundumos és annál rövidebb mérések a kétimpulzusos módszerek újbóli elterjedését hozták magukkal. A 6. ábra egy ilyen berendezés vázlatos rajzát mutatja. Az elrendezés egyben a kémiai kísérletekben alkalmazott ultragyors festéklézereknek is egy tipikus példája. Az erõsítésre használt Nd:YAG (neodímiummal szennyezett yttrium-alumínium gránát) lézer nagyenergiájú célokra jól alkalmazható a gránát jó hõvezetése miatt. A nagy energiára a lézerkinetika szempontjából egyrészt azért van szükség, hogy az impulzus rövid idõtartama alatt elegendõ számú molekula gerjesztõdjön, másrészt azért, hogy a kontinuum elõállításához szükséges nemlineáris optikai folyamatok elõidézéséhez elegendõen nagy legyen a fényintenzitás.
A nemlienáris optikai úton elõállított fehér kontinuum csak annyi ideig „világít", ameddig a nemlineáris közegben elegendõen nagy a fényintenzitás - ez pedig nem hosszabb mint, az impulzus idõbeli szélessége. Történetileg elõször Alfano és Shapiro mutatták ki a fehér kontinuumot folyékony argonban és kriptonban [21], de hamarosan kitûnt, hogy az ultragyors spektroszkópiában a H2O és D2O is megfelelõ nemlineáris közegek fehér kontinuum generálására [22, 23].
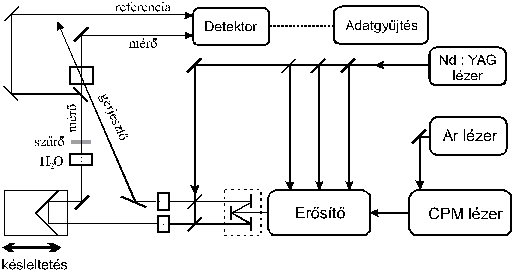
6. ábra. Festéklézer alkalmazása ultragyors kinetikai mérésekben [20]. Az ábra "mûködõ változata" is megnézhetõ. A CPM lézer pumpálását egy nagyteljesítményû Ar-ionlézer végzi. Az 5. ábrához hasonló gyûrûs elrendezésû CPM lézer kimenõ impulzusa 60 fs szélességû, 620 nm hullámhosszú, és kb. 1 nJ energiájú. Ezt erõsítik az egymástól abszorbeáló festéksugárral elválasztott, erõsítõ festéket tartalmazó küvetták, amelyeket 10 Hz ismétlési frekvenciával Q-kapcsolt Nd:YAG lézerrel pumpálnak. (a pumpáló fényimpulzusok a lézer 532 nm hullámhosszú második felharmonikusai.) A rácsokkal történõ impulzus-összenyomás olyan új megoldást tartalmaz, amelyhez az elsõ rácsról mindkét irányban nyert elsõrendû diffrakciós maximumot hasznosítják [20]. Az egyiktõl a sávszûrõvel szûkített spektrális szélességû 620 nm-es impulzust a mintát tartalmazó küvettába vezetik, ahol kb. 10 TW/cm2 fényteljesítménnyel indítja a reakciót. A másik sugárnyalábot is még egyszer erõsítik az összenyomás után, majd egy D2O-t tartalmazó küvettába fókuszálják, ahol nemlineáris optikai jelenségek következményeként fehér fény (ún. kontinuum) keletkezik. Ez a fehér mérõ fényimpulzus elõbb áthalad a kettõs tükrös késleltetõn, majd a gerjesztõ impulzussal kis szöget bezárva áthalad a küvettán. A mért abszorbancia a spektrofotométerben detektált jelbõl meghatározható. A detektálást és a késleltetés beállítását számítógép végzi, amely egyúttal a mért adatokat is rögzíti.
Ultragyors lézerkinetikai célokra újabban egyre gyakrabban alkalmaznak szilárdtestlézer-erõsítõket is. Erre példa a 11. ábrán látható.
Az ultragyors lézerkinetikai
mérésekhez tehát ugyanabból a lézerbõl
származó két impulzusra van szükség, amelyek
egyike, a kívánt reakciót kiváltó gerjesztõimpulzus
nagy energiájú és monokromatikus, míg a másik
az abszorpció mérésére alkalmas, széles
spektrális tartományú kontinuum. Az idõmérés
a két impulzus reakciótérbe érkezése
közötti idõ beállítását jelenti
a kettõs tükör által kijelölt fényút
hosszának megfelelõ beállításával.
A 6. ábrán látható elrendezés lehetõvé
teszi, hogy a fényút-hossz változtatásakor
a beesés iránya ne változzon. Míg a nanoszekundumos
mérések esetében a problémát a túl
hosszú fényút jelentette (30 cm /1
ns), addig itt a helyzet fordított; az igen kicsi fényútkülönbségek
(0,3 mm/1
fs) pontos beállítását kell megoldani. Ehhez
a késleltetõ tükröket egy precíziós
mikrométercsavar segítségével állítható
sínre szerelik, a mikrométercsavart pedig egy léptetõmotorral
forgatják. Az így elérhetõ pontosság
kb. 0,1 mm,
ami az egy femtoszekundum pontosságú idõbeállítást
éppen lehetõvé teszi. A két impulzus ilyen
pontosságú szinkronizálása azonban csak relatíve
lehetséges, a két impulzus pontos átfedése
által kijelölt nulla idõkülönbséget
minden kísérletben külön meg kell határozni.
Ennek következményeire késõbb még kitérünk.
Megjegyezzük még, hogy a mikrométercsavar-mechanika
miatt ezekkel a berendezésekkel néhányszor tíz
pikoszekundumnál (10-20 cm) hosszabb idõket általában
nem szokás mérni.
3.2. A kétimpulzusos
mérési adatok értelmezése
Az olvasó elcsodálkozhat azon, hogy miért kell külön foglalkozni az ultragyors mérések értelmezésével. Ennek azonban egyszerû oka van: az igazán érdekes - valós idejû detektálási módszerekkel nem mérhetõ - ultragyors reakciók lejátszódásához szükséges idõ olyan rövid, hogy ahhoz képest az impulzusok hossza nem elhanyagolható, sõt, gyakran azzal összemérhetõ. Másképpen fogalmazva ez azt jelenti, hogy mind a gerjesztõ, mind a mérõ impulzus szélességének megfelelõ idõ alatt a tanulmányozott reakció elég jelentõs mértékben elõrehalad. Ilyenkor figyelembe kell venni, hogy a reakciót nem pillanatszerûen indítja a gerjesztõimpulzus, hanem a szélességének megfelelõ idõintervallumban állandóan indulhat a reakció, és hasonlóképpen a detektálás sem pillanatszerû. A detektált jel kvantitatív értelmezésének részleteit a 7. ábra jelöléseinek felhasználásával abszorpciós detektálás esetére mutatjuk be. Induljunk ki ehhez a fényabszorpciót leíró Lambert-Beer törvénybõl:
I = I0 · 10 - ecl = I0 · e - ln 10 ecl (3.1)
A képletekben I0 a detektálás irányában beesõ, I pedig ugyanebben az irányban kilépõ fényintenzitás, e a dekadikus moláris abszorpciós együttható, c az abszorbeáló anyag koncentrációja, l pedig a fény optikai úthossza az abszorbeáló anyagban. Ha az ecl kitevõ megfelelõen kicsi, akkor a 3.1 kifejezés
I = I0 (1 - ln10 ecl -1/2 ( ln10 ecl)2 - …) (3.2)
Taylor-sorában elegendõ az elsõfokú tagig elmenni. Ahhoz, hogy ennek egyszerûsítõ következményeit ki lehessen használni, célszerûen a DOD-vel jelölt abszorbancia-különbséget szokás detektálni, amit gyakran differenciális optikai denzitásnak neveznek:
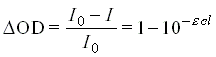
Ez a sorfejtésbõl csak az elsõfokú tagot figyelembe véve az
DOD 1 - (1 - ln10 ecl) = ln10 ecl (3.4)
alakban írható fel. Az egzakt 3.3 exponenciális és a közelítõ 3.4 lineáris kifejezés értékei között az eltérés DOD 0,1 esetén még csak mintegy 0,5%, az 1%-ot DOD 0,15-nál éri el, 0,01-0,05 abszorbancia-különbség tartományban pedig 0,15% alatt van. Ebben a tartományban tehát megfelelõ a 3.3 lineáris közelítés.
Vizsgáljuk meg, hogyan alkalmazható ez ultragyors kémiai reakciók nyomonkövetésére. Ha a reagáló rendszerben a reakciót a 7. ábra Ig(t) gerjesztõ impulzusával indítjuk, a mérést pedig a
7. ábra. Jelölések az ultragyors mérésekben detektált integrált intenzitás számításához.
gerjesztõ impuzust tidõ
múlva követõ
fényimpulzussal mérjük, akkor a t idõpillanatban
indított reakció t' idõpillanatban elképzelt
detektálásakor - azaz t'- t reakcióidõ
múltán - a reakciótermékek okozta fénygyengítés
(3.5)
A lineáris közelítés alkalmazásával ez átírható az
(3.6)
alakba, amivel kifejezhetõ a megfelelõ DOD:
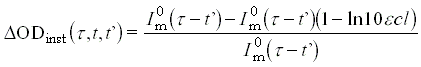
ami éppen ln10
ecl
eredményt ad. Az
azonban idõfüggõ, ezért a különbözõ
t' idõpillanatokban az
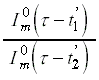
függvényt annak -¥
és +¥
között számított integráljával. Az
így kapott Im ( t-t'
) függvényre
teljesül az
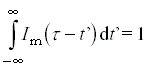
feltétel, tehát az Im( t-t' ) függvény kezelhetõ úgy, mint a detektálás valószínûségi sûrûségfüggvénye adott t' idõpillanatban. Ennek segítségével felírhatjuk az Ig(t) gerjesztõimpulzus által t' idõpillanatban generált kiindulási anyagokból kialakuló reakcióelegyben a teljes mérõimpulzus ideje alatt integrált DOD értéket:
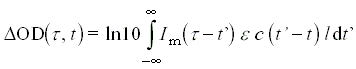
A fenti egyenletben tehát az Im ( t-t' ) függvény már nem fényerõt jelent, hanem a fényerõ idõbeli eloszlásának valószínûségi sûrûségfüggvényét. (Mivel a fényerõ maga a 3.7 egyenletben úgyis kiesik, ezért annak abszolút értékére nincs is szükség.)
A fentiekhez hasonlóan vehetjük figyelembe a gerjesztés hatékonyságának idõbeli eloszlását is. Ha az Ig(t) függvényt is 1-re normált valószínûségi sûrûségfüggvénynek tekintjük, akkor a teljes gerjesztõ impulzus hatására keletkezõ c(t') koncentráció t' idõpillanatban a
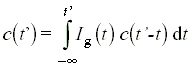
integrállal számítható. Ez azonban valószínûségszámítási értelemben nem jól kezelhetõ kifejezés. Ehelyett használhatjuk az azonos eredményt adó
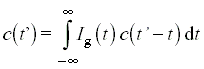
kifejezést, amelyben a c(t'- t ) függvényt úgy értelmezzük, hogy annak értéke t > t' esetén azonosan zérus (ami ettõl függetlenül is a függvény korrekt értelmezése a reakciókinetikában, hiszen negatív reakcióidõkre a t = 0 idõpillanatban induló reakció okozta változás zérus). Ez a kifejezés egyúttal matematikailag is könnyebben kezelhetõ, mivel a 3.9 és 3.11 egyenletek kombinálásával kapott
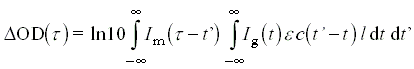
szerkezetû integrálok könnyen átfogalmazhatók a konvolúció felhasználásával. Definíció szerint f és g függvények konvolúciója:
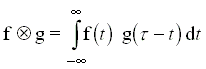
Hasonlóképpen definiálható g és h függvények korrelációja is:
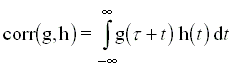
Ez utóbbi felírható
konvolúciós integrálként is, ha a g függvény
idõtengelyét megfordítjuk. A fordított idõtengelyû
függvényt beírva
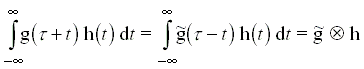
A fentiek figyelembevételével a 3.12 egyenletbõl kiindulva kihasználjuk az integrálás sorrendjének felcserélhetõségét (vagy a megfelelõ konvolúciók kommutativitását és asszociativitását), így azt az alábbi alakban is írhatjuk:
(3.16)
Szövegesen ezt úgy fogalmazhatjuk meg, hogy a detektált differenciális optikai denzitás a gerjesztõ és mérõ impulzus korrelációjának konvolúciója az ecl pillanatnyi differenciális optikai denzitással. Ez utóbbi az a DOD függvény, amit egy egyszerû, konvolúció nélküli kísérletben mérhetnénk a reakcióidõ függvényében. Megjegyzendõ, hogy ha nem egyetlen abszorbeáló anyag van a reakcióelegyben, aminek koncentrációja a reakció során változik, akkor az ecl helyén egyszerûen a megfelelõ függvények összege, eici l szerepel. Ebben a függvényben tehát - eltekintve az ismert l optikai úthossztól - az ei moláris abszorpciós együtthatók, illetve a koncentrációváltozást leíró ci (t) függvények szorzata szerepel. Ezt az összeget nevezzük a késõbbiekben kinetikai válaszfüggvénynek. A konvolúcióban szereplõ másik függvény a két impulzus korrelációja, amely kísérletileg meghatározható - legalábbis abban az esetben, ha a két impulzus hullámhossza megegyezik [24].
8. ábra. A kétimpulzusos módszerrel detektált kinetikai görbe kialakulásának szemléltetése. a) Az effektív impulzus a gerjesztõ és mérõ impulzusok, valamint a csoportsebesség-diszperziót leíró négyszögfüggvény konvolúciója. b) A detektált görbe az effektív impulzus és a kinetikai válaszfüggvény konvolúciója.
A kinetikai gyakorlatban ez ritkán teljesül, hiszen egy adott reakciót általában egyetlen alkalmas (szelektív) gerjesztõ hullámhosszúságú fénnyel érdemes indítani, de a spektrális információk érdekében minél több különbözõ hullámhosszon kell detektálni a tranziens differenciális optikai denzitást. Ebben az esetben a két impulzus korrelációját még kiszélesíti a törésmutató diszperziójából a két hullámhosszon az adott közegben a fény terjedési sebességében adódó különbség hatása. (Ez 5 mm-es, vizet tartalmazó küvettában 100 fs impulzusszélesség esetén akár további 100 fs-mal szélesítheti a két impulzus korrelációját.) Az így kialakuló, a fénysebesség-különbség hatását is magában foglaló korrelációs függvényt nevezzük effektív impulzusnak. Ennek alakja általában megegyezik a kísérletileg meghatározható korrelációfüggvény alakjával, csak az elõbb említett hullámhossz-különbség miatt annál szélesebb. A detektált jel konvolúciós természetét a 8. ábrán grafikusan szemléltetjük.
Az ultragyors lézerfotolízis során az elõbbieken túlmenõen felléphet még egy „komplikáció". Az alkalmazott igen nagy fényteljesítmény sûrûségek (~1012 W/cm2) következtében gyakran elõforduló többfoton-abszorpció. Ilyenkor egy adott molekula egyszerre több fotont is abszorbeál. Ennek következménye többek között az is, hogy a gerjesztés hatásfoka nem az Ig(t) függvénnyel, hanem annak valamely [Ig(t)]n hatványával írható le. Ideális esetben ez a kitevõ megegyezik az egyszerre abszorbeált fotonok számával, de n > 2 esetén általában annál kisebb. A kitevõ pontos értéke kísérletileg a fényintenzitás változtatásával meghatározható [25]. Többfoton-abszorpció esetén tehát a 3.16 egyenletben a megfelelõ kitevõjû gerjesztõ intenzitás konvolúciójával keletkezik az effektív impulzus.
A fentiekben abszorpciós detektálás
esetére mutattuk be az ultragyors kétimpulzusos jel kialakulását.
Ha nem abszorbanciát, hanem lézerindukált fluoreszcenciát
(LIF) detektálnak, akkor a leírás lényegében
ugyanolyan eredményt ad. Az LIF-jel úgy jön létre,
hogy a kiváltó lézerfény elõször
abszorbeálódik, majd az ily módon gerjesztett molekula
fluoreszkál. Két vagy többatomos molekulák, ill.
gyökök esetén a kibocsátott fluoreszcencia általában
más hullámhosszú, mint az elnyelt fény. Ilyenkor
a beesõ fénytõl eltérõ irányban
detektált fluoreszcenciából jól kiszûrhetõ
a szórt gerjesztõ fény, így a módszer
nagyon érzékennyé tehetõ. Összefoglalva,
a LIF-jel intenzitása arányos az elnyelt gerjesztõ
fény intenzitásával, tehát a fenti levezetés
ugyanúgy érvényes, azzal a különbséggel,
hogy a detektált intenzitás emisszió, azaz a reakció
hatására az intenzitás minidig növekszik, míg
abszorpciós mérés esetén gyakran csökken.
Megjegyezzük még, hogy míg az abszorbancia mérése
- abban az esetben, ha az abszorbeáló molekula moláris
abszorpciós együtthatója más mérésekbõl
ismert - alkalmas abszolút koncentrációk meghatározására,
addig ez a LIF-módszer esetén csak kalibrációval
lehetséges. A gyakorlatban azonban az ultragyors abszorbanciamérések
is csak relatív koncentrációmeghatározást
tesznek lehetõvé, mivel a pikoszekundumnál rövidebb
ideig élõ anyagfajták moláris abszorpciós
együtthatója nem meghatározható. Vannak olyan
ultragyors reakciók, amelyeknek terméke hosszú élettartamú
(legalább
100 ps körüli), ezek kinetikai görbéiben a hosszú
idõ után állandósult termékkoncentráció
lehetõséget nyújt a termék ismert moláris
abszorpciós együtthatójához történõ
kalibrálásra.
3.3. A detektált
kinetikai görbék dekonvolúciója
Az elõzõ alfejezetben láttuk, hogy az „ultrarövid" idõ alatt felvett kinetikai görbék nem értelmezhetõk a konvolúció figyelembe vétele nélkül. A konvolúció hatását a 9. ábrán szemléltetjük, ahonnan látható, hogy a kinetikai differenciálegyenlet-rendszerek megoldásaként kapott koncentrációprofilok idõben „szétfolynak", azaz a konvoluált görbéknek mind a felfutása, mind a lecsengése lassúbb lesz. Ha azt is figyelembe vesszük, hogy általában a kiindulási anyagok, köztitermékek és végtermékek egyaránt abszorbeálnak, akkor az azok összegeként detektált kinetikai görbén nem igazán látható, hogy milyen mechanizmus szerint zajlott le az adott reakció. A helyzetet tovább bonyolítja az is, hogy gyakran maga az effektív impulzus sem könnyen meghatározható, így a konvolúció kvantitatív figyelembevétele további nehézségekbe ütközik.
A konvolúció hatását a dekonvolúciónak nevezett eljárással lehet kiküszöbölni. Ehhez úgy kellene megoldani a 3.12 vagy 3.16 integrálegyenleteket, hogy a konvoluálatlan kinetikai görbéket kapjuk vissza. A dekonvolúció a legkézenfekvõbb, direkt módon a 3.16 egyenlet alapján végezhetõ el. Írjuk át ezt az egyenletet a
DOD = Ieff finst (3.17)
alakba, ahol Ieff az effektív inpulzusfüggvény, finst pedig a (konvoluálatlan) kinetikai válaszfüggvény. A 3.17 egyenlet Fourier-transzformáltja felírható
FT(DOD) = FT(Ieff)· FT(finst) (3.18)
alakban, mivel a konvolúció Fourier transzformáltja éppen a konvoluált függvények Fourier transzformáltjainak szorzata [26]. A Fourier transzformáció az alábbiak szerint értelmezhetõ:
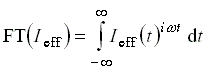
9. ábra. A konvolúció hatása kétimpulzusos módszerrel detektált jelre kiindulási anyag, köztitermék és végtermék detektálása esetén. A szaggatott vonallal jelzett pillanatnyi abszorbancia-függvények zérus késleletetéstõl indulnak, a 300 fs félszélességû effektív impulzussal konvoluáltak (folytonos vonalak) negatív késleltetéstõl.
A Fourier-transzformációt értelmezhetjük úgy is, hogy egy f(t) függvényt az idõtartományból a frekvenciatartományba képez le, így az F(w) Fourier transzformált éppen az f(t) függvény frekvenciaspektrumát adja az w körfrekvencia függvényében. Visszatérve a dekonvolúcióra, azt mondhatjuk tehát, hogy a 3.18 egyenletbõl kifejezhetõ a kinetikai válaszfüggvény Fourier transzformáltja:
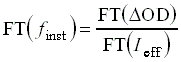
Ennek inverz Fourier transzformáltja pedig elvileg éppen a konvoluálatlan finst kinetikai válaszfüggvényt adja. Elvileg, mert a gyakorlati megvalósítás egyelõre nehézségekbe ütközik. Az egyik probléma az, hogy az Ieff effektív impulzus általában egy Gauss-szerû függvény, aminek a frekvenciatartományban csak kevés, zérushoz közeli frekvenciakomponense van, ezért a 3.20 egyenlet jobb oldalán a függvények értékeinek elõállításához igen gyakran nullával kellene osztani. Ezt a problémát úgy lehet kikerülni, hogy az Ieff Fourier transzformáltjához hozzáadunk egy kis „fehér zajt", de ez természetesen megjelenik az osztás eredményében is, azaz eltorzítja a kiszámítandó kinetikai válaszfüggvényt, amit az inverz Fourier transzformáció elvégzése elõtt egy szûréssel a lehetõ legkisebb mértékûre kell csökkenteni. A másik probléma az, hogy a Fourier transzformáció csak periodikus függvényekre végezhetõ el, ami esetünkben azt jelenti, hogy a kinetikai görbéknek, amik a DOD képzése miatt zérusról indulnak - zérushoz kell visszatérniük a mérés végén. A 9. ábrán azonban látható, hogy ez termékjellegû görbe esetén egyáltalán nem teljesülhet, de a gyakorlatban kiindulási anyagok és köztitermékek esetén sem mérünk olyan hosszú ideig, amíg a görbék zérusig lecsengenének. Ennek a problémának a kezelése már nem egyszerû. Ha a Fourier transzformációt el akarjuk végezni, akkor a görbék végét ki kell egészíteni egy zérushoz lecsengõ „farokkal", ami viszont zavaró frekvencia-komponenseket visz a frekvenciaspektrumba, ezért eltorzítja a kapott dekonvoluált kinetikai válaszfüggvényt is. Ennek a problémának eredményes kezelésével a szerzõ kutatócsoportja foglalkozik. A megoldás egyelõre csak számított, zajmentes DOD görbék esetén mûködik [27], zajos kísérleti adatokra még ki kell dolgozni egy iterációs szûrõoptimalizálási eljárást [28].
A direkt Fourier transzformációval végzett dekonvolúció igen elõnyös tulajdonsága, hogy - legalábbis ismert Ieff impulzusfüggvény esetén - önkényes feltételezések nélkül juthatunk hozzá a konvoluálatlan kinetikai görbéhez, nagyon kis numerikus számításigénnyel. Azonban - amint az a fentiekbõl kiderült - ez a módszer egyelõre nem mûködõképes. A jelenleg mûködõ, és elterjedten használt módszert szokás rekonvolúciónak is nevezni [29, 30]. Ennek során feltételezünk egy konkrét kinetikai mechanizmust, elõállítjuk az ahhoz tartozó koncentráció-idõ függvényeket, azokból kiszámítjuk az finst kinetikai válaszfüggvényt, amit beírunk a 3.12 integrálegyenletbe. Az így kapott DOD modellfüggvényben szereplõ kinetikai és fotofizikai paramétereket azután nemlineáris legkisebb négyzetes módszerrel megbecsüljük. A becslés egy iterációs eljárás, amelyben megkeressük azokat a paramétereket, amelyek minimalizálják a

eltérésnégyzet-összeget. Az összegzésben a j index a mérési pontokon (beállított késleltetéseken) fut végig, az i index pedig a (különbözõ hullámhosszakon detektált) kinetikai görbéken. Ez utóbbi azért fontos, hogy az összes mért DOD szimultán kiértékelésével a paraméterek becsléséhez a lehetõ legtöbb információt egyszerre használjuk fel. A wij súlyok a megfelelõ mérési pont statisztikai súlyát jelentik. A statisztikából tudjuk, hogy a legkedvezõbb tulajdonságú (minimum variancia torzítatlan) becslést akkor kapjuk, ha a wij súlyok éppen a megfelelõ mért értékek szórásnégyzetének reciprokai [31, 32]:
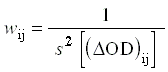
A lézerkinetikai méréseknél a súlyok meghatározása könnyû, hiszen tipikusan több száz impulzus átlagolásával mérnek meg egyetlen (DOD)ij értéket, ezért az átlag mellett annak szórása is egyszerûen kiszámítható a mérés során.
A fenti rekonvolúciós módszernek van két nagy hátránya. Ezek közül a nagyobb hátrány az, hogy a dekonvolúcióhoz eleve szükséges egy - gyakran önkényes - reakciómechanizmus feltételezése. A másik hátránya az, hogy a paraméterbecslés során minden egyes iterációs lépésben sokszor ki kell számítani a konvolúciót is tartalmazó modellfüggvény értékeit, ami igen számításigényes feladat. (Igaz, hogy eközben egyúttal a modellfüggvény paramétereinek becsült értékeit is megkapjuk.) Példaképpen említhetem egy közepesen bonyolult mechanizmus rekonvolúciós kiértékelését tíz kinetikai görbébõl, amelyek egyenként kb. 100 mérési pontot tartalmaznak. Ehhez tipikusan tíz óra nagyságrendû gépidõre van szükség egy RISC/6000 számítógépen, míg ugyanez direkt Fourier dekonvolúcióval és azt követõ paraméterbecsléssel egy percen belül lefutna ugyanazon a gépen, vagy néhány perc alatt egy szerényebb személyi számítógépen is.
A rekonvolúció nagy számításigénye és nehézkes elvégezhetõsége (nem könnyû megfelelõ kiindulási paramétereket találni az iterációs becslés indítására, hogy valóban megtalálja az eljárás a megfelelõ minimumot) miatt több szerzõ gyakran él indokolatlan, önkényes egyszerûsítésekkel. Gyakori a kinetikai modell túlzott egyszerûsítése, és általánosan elterjedt gyakorlat az is, hogy csak egy, vagy igen kisszámú kinetikai görbe kiértékelését végzik el. Kimutatható azonban, hogy ez jelentõs információveszteséggel jár, és hamis következtetések levonásához vezethet [33].
A rekonvolúció eredményeként - mint általában legkisebb négyzetes paraméterbecslés esetén - kapott becsült paraméterek többé-kevésbé korreláltak. Ha az eljárás során egyúttal az impulzus paramétereit is becsüljük, akkor azok is korrelálhatnak a kinetikai és fotofizikai paraméterekkel. Ennek az lehet a következménye, hogy a becsült impulzusparaméterek eltérését a valódi értéktõl a kinetikai paraméterek megfelelõ eltérései kompenzálhatják. Az impulzus alakjának pontos meghatározásával ez a határozatlanság elkerülhetõ.
Az effektív impulzus alakja célszerûen két módszerrel határozható meg. A 8. ábrán látható, hogy ez az impulzusalak nem csak a gerjesztõ és mérõ impulzusoktól függ, hanem a törésmutató-diszperzió következtében a két különbözõ hullámhosszú fényimpulzus között fellépõ csoportsebesség-különbségtõl is. Az impulzusalak pontos meghatározása tehát csak ugyanolyan kísérletben lehetséges, mint amilyenekben a kinetikai mérések folynak, beleértve a mintatartó küvettában lévõ közeget is. Az impulzus meghatározásának egyik módszere indirekt; a mintatartó küvettában egy ismert fotokémiai reakciót vizsgálnak ugyanabban a közegben (oldószerben vagy inert gázban), mint amiben a tulajdonképpen tanulmányozni kívánt reakciót. A 3.17 egyenlettel leírható konvolúcióban ilyenkor az finst kinetikai válaszfüggvény ismert, és az Ieff effektív impulzus paramétereit (vagy ha nem ismert, akkor próbálgatással az alakját is) kell meghatározni. Ennek a módszernek több hátránya is van. Gyakran nehéz megoldani, hogy a reakcióelegy ne legyen a mintában, de törésmutató-diszperzió szempontjából a közeg ugyanolyan legyen. (Kiváló példa erre tiszta anyagok fotolízisének vizsgálata.) Ugyancsak problémát jelent, hogy kevés olyan fotokémiai reakció van, amelynek viselkedése megfelelõ pontossággal ismert lenne - hiszen azt éppen ultragyors lézerfotolízissel kellene meghatározni. Amíg az impulzusok néhány száz femtoszekundum szélesek voltak, erre a célra „pillanatszerûen" gerjesztõdõ festékeket használtak, amelyeknek fényelnyelõ gerjesztett állapota az impulzusalak mérésénél sokkal hosszabb ideig fennmarad. A 8. ábra alsó sorában ekkor a kinetikai válaszfüggvényt egy egyszerû lépcsõfüggvényként lehet értelmezni [34]. Az impulzusok keskenyedésével azonban hamar kiderült, hogy ezek a lépcsõfüggvények a valóságban nem egy derékszögû „ugrással" írhatók le, hanem valamilyen idõállandóval futnak csak fel, amely általában néhányszor tíz femtoszekundum. Az effektív impulzusalak meghatározása ezzel a módszerrel ezért nem megbízható.
A másik módszer ezt a problémát azzal küszöböli ki, hogy az impulzusalak meghatározásához olyan jelenséget használ fel, amelynek válaszideje femtoszekundumos idõskálán valóban „pillanatszerû", és válaszfüggvénye nem egy lépcsõfüggvény, hanem egy Dirac-delta függvény. Ha ezt konvoluáljuk az effektív impulzussal, akkor detektált jelként magát a változatlan effektív impulzust kapjuk. Erre a célra alkalmazható pl. a Raman-szórás vagy a stimulált Raman emisszió [20]. Folyadékokban elég sûrûn találhatunk Raman spektrumvonalakat, és az ultrarövid impulzusok több száz gigawattos teljesítménye ezeket általában megfelelõ intenzitással gerjeszti is. A Raman emisszió vagy abszorpció megjelenése gyakran „in situ" impulzusalak-meghatározást is lehetõvé tesz, hiszen a pillanatszerû effektus következtében megjelenõ, késleltetés nélkül felfutó és lecsengõ effektív impulzus dekonvolúció nélkül kiolvasható a detektált jelbõl.
Ha sikerül olyan hullámhosszat találni adott folyadék esetén, ahol többfotonos elnyeléssel sem játszódik le reakció, de megjelenik a Raman effektus, akkor az effektív impulzus alakja közvetlenül detektálható. Ezzel a módszerrel sikerült kimutatni, hogy a 6. ábrán látható lézerberendezés impulzusai sech2 alakúak [35]. A meghatározás alapjául szolgáló detektált görbe és az illesztett impulzusalak a 10. ábrán láthatók.
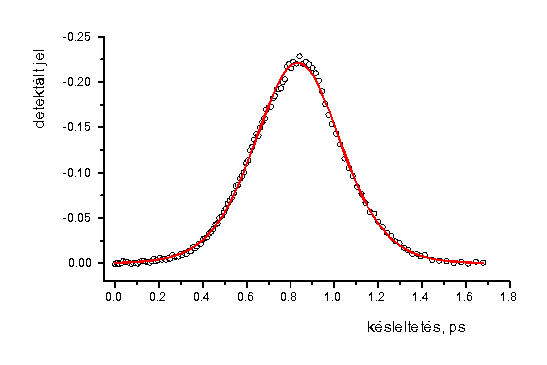
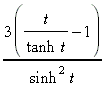 illeszkedett szisztematikus eltérések nélkül;
ez látható az ábrán. Az illesztett effektív
impulzus szélessége félmagasságban 456 fs.
(A gerjesztõ, illetve mérõ impulzusok szélessége
ennek megfelelõen kb. 200 fs.)
illeszkedett szisztematikus eltérések nélkül;
ez látható az ábrán. Az illesztett effektív
impulzus szélessége félmagasságban 456 fs.
(A gerjesztõ, illetve mérõ impulzusok szélessége
ennek megfelelõen kb. 200 fs.)
Ha a femtoszekundumok tartományában kinetikai méréseket akarunk végezni, elengedhetetlen két lézerimpulzus egymáshoz képest történõ késleltetésének felhasználása az idõ meghatározására. Amíg az egyik impulzus a reakciót indítja, addig a másikkal pl. meg lehet mérni a reakció során bekövetkezõ abszrobancia-változást. Amennyiben a mérési elrendezésünk ennél az egyszerû sémánál bonyolultabb, akkor kettõnél több impulzus alkalmazására is szükség lehet.
Az egyik ilyen eset az, amikor pl. igen
rövid élettartamú tranziens anyagok jól definiált
gerjesztett állapotainak spektrumát akarjuk tanulmányozni.
Tegyük fel, hogy egy ultragyors folyamatban keletkezõ átmeneti
termék kioltási folyamatokban nanoszekundumos idõskálán
elreagál. Ezen köztitermék egy megfelelõ hullámhosszú
és intenzitású ultragyors lézerimpulzussal
(ez a szintetizáló impulzus) elõállítható,
majd megfelelõ (1 ns körüli) fix késleltetés
után belõtt impulzussal (ez a gerjesztõ impulzus)
szelektíven gerjeszthetõ, végül a gerjesztett
tranziens spektruma egy változtatható késleltetésû
és hullámhosszúságú mérõ
impulzussal meghatározható.
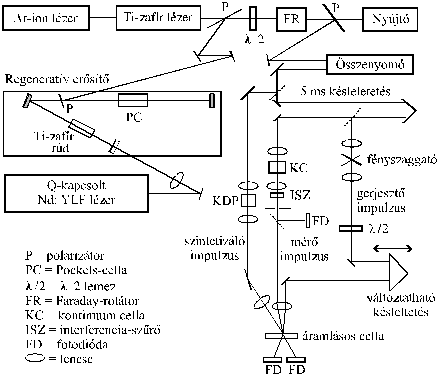
11. ábra. Ti-zafír lézerek alkalmazása háromimpulzusos mérésekben [36]. Az argonion-lézer által pumpált Ti-zafír lézer 770 nm hullámhosszúságú, 100 fs széles, néhány nJ energiájú impulzusokat bocsát ki, amelyeket ~130 ps szélesre nyújtanak. A nyújtott, széles spektrális sávú impulzusokat a Q-kapcsolt Nd:YLF lézer által pumpált Ti-zafír regeneratív erõsítõben (ahol az erõsített impulzusok mintegy 30-szor haladnak át) kb. 0,5 mJ energiájúra erõsítik, majd rácspár segítségével újra összenyomják. Összenyomás után 2 kHz ismétlési frekvenciával kb. 180 fs széles, 770 nm hullámhosszúságú impulzusokat kapnak. Ennek egy részébõl keletkezik a frekvenciakétszerezõ KDP kristályon áthaladva a 385 nm hullámhosszú szintetizáló impulzus, másik részét pedig fix 5 ns késleletetés után kettéosztják. A gerjesztõ impulzus változtatható késleltetés után jut az áramló reakcióelegybe, a mérõimpulzus pedig a kontinuum cellában keletkezõ fehér fénybõl az ISZ interferenciaszûrõvel kiválasztott hullámhosszúságú fény.
Ezzel a módszerrel a gerjesztett állapot spektruma is és élettartama is meghatározható. Példaként a 13. ábrán bemutatjuk azt a mérési elrendezést, amelyet az
(3.23)
fotodisszociációs reakció
termékének gerjesztésére, és a gerjesztett
termék spektrumának idõbeli nyomonkövetésére
használtak [36]. A szintetizáló impulzus hatására
keletkezõ az etanolban
stabil szolvatált részecskeként él egészen
addig, amíg rekombinálódik egy jódatommal.
Ez a rekombináció azonban igen lassú, diffúziókontrollált
folyamat, amely a résztvevõ nehéz részecskék
miatt néhány nanoszekundum alatt csak észrevehetetlen
mértékben játszódik le, így a kísérletekben
a gerjesztõ impulzus gyakorlatilag a teljes képzõdött
koncentrációt látja.
A szintézis-gerjesztés-mérés három impulzusa nem az egyetlen példa háromimpulzusos módszerek alkalmazására. A lézerimpulzusok koherenciáját és nagy teljesítményét kihasználó módszerek alkalmazásakor általában két - koherens - impulzus idézi elõ a kívánt effektust, a kinetikai információhoz pedig egy harmadik, idõben késleltetett impulzussal lehet hozzájutni. Egyik példa erre az indukált tranziens rács módszer [37]. Ehhez a gerjesztõ impulzust kettéosztják, és úgy vezetik be a mintába, hogy oda egymással adott szöget bezárva, pontosan átfedve érkezzenek. (Ez úgy érhetõ el, hogy az egyik fényútba finoman változtatható késleltetést építenek be.) A két koherens nyaláb között ekkor a mintában interferencia lép fel, és az így keletkezõ intenzitás-eloszlásnak megfelelõ gerjesztés okozta optikai változás következtében egy optikai rács alakul ki. A késleltetett mérõimpulzus ezen a rácson diffrakciót szenved. A detektort az ily módon szórt fény elsõ rendû maximumának irányában helyezik el. A szórt fény intenzitásának mérésével idõben nyomonkövethetõ a rács kialakulása és megszûnése, ami a gerjesztésre és az azt követõ folyamatokra nézve szolgáltat kinetikai információt.
Befejezésként még
megemlítjük, hogy a 90-es évek közepétõl
lehetõség nyílt arra is, hogy nagyfrekvenciájú
optoelektronikai berendezések segítségével
két - egyébként egymástól függetlenül
mûködõ lézer impulzusait szinkronizálják.
Ez nagy távlatokat nyit a kinetikai alkalmazások elõtt,
mivel lehetõvé teszi elvileg bármilyen hullámhosszú
lézerimpulzusok kombinálását egy két-
vagy háromimpulzusos mérés során. A megfelelõ
kísérletek eredményeirõl e dolgozat írásakor
azonban közlemények még nem hozzáférhetõk.
Irodalmi hivatkozások
és megjegyzések